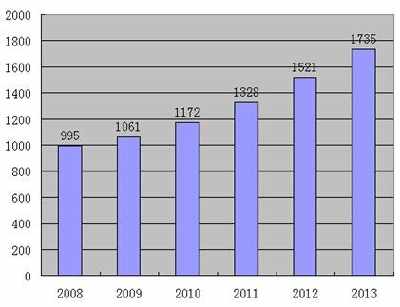
用画画解决问题,是孩子打开解决问题大门的一把“金钥匙”。其实很多问题都是可以快速解决的,比如几何问题、距离问题。如果光靠思考很难想出答案,画画一目了然。在这里,我们将整理出六种小学数学图片的图形答案,为孩子们收集起来。
01
平面图
对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题,可以借助画平面图帮助思考解题。
例1有两个自然数A和B,如果A增加12,B不变,则积增加72。如果A不变,如果B增加12,则积增加120。求原来两个数的乘积。
根据题目条件的抽象特征,建议用矩形图将条件转化为因素与产品的关系。先画一个长方形,长A,宽b,这个长方形的面积是原来两个数的乘积。如图(1)所示。
根据条件,如果A增加12,长度将延长12,B的宽度保持不变,如图(2)所示。同样,如果A不变,也就是长度不变,如果B增加12,宽度就会延长12,如图(3)所示。从图中不难发现:
原始矩形的长度(a)为120 12=10
原始矩形的宽度(b)为72/12=6。
两个数的乘积是10 6=60。
借助矩形图,阐明了问题中的条件,找到了解决问题的关键。
例2梯形的下底是上底的1.5倍。上底座延伸4厘米后,梯形变成了面积为6平方厘米的平行四边形。原来的梯形面积是多少平方厘米?
根据标题的意思画一张平面图:
从图中可以看出,上底和下底的差是4厘米,这个4厘米正好对应1.5-1=0.5倍。因此,如果上底为4 (1.5-1)=8 (cm),下底为8 1.5=12 (cm),高度为60 12=5 (cm),那么原梯形的面积为(812)52=5o(cm2
02
立体画
一些求积题,结合题目的内容画出立体图,这样做,使题目的内容直观、形象,有利于思考解题。
例1把一个立方体切成两个长方体,表面积增加了8平方米。原始立方体的表面积是多少平方米?
凭想象做这件事更难。根据问题的意思画画可以帮助我们思考并找到问题的解决方案。根据标题的意思画一个立体图:
从图中不难看出,表面积增加了8平方米,实际上是增加了2个正方形面,每个面的面积为8 2=4(平方米)。原立方体有六个面,即表面积为4 6=24(平方米)。
例2做了一个长3厘米、宽2厘米、高1厘米的大长方体。这个大长方体的表面积是多少?
根据标题的意思,画一个透视图,说明有三种由三个长方体组成的大长方体。
(1)长方体长2 3=6(厘米),宽3厘米,高1厘米。表面积为(6 3 6 1 3 1 ) 2=54 (cm2)。
(2)长方体长3 3=9(厘米),宽2厘米,高1厘米。表面积为(9 2 9 1 2 1 ) 2=58 (cm2)。
(3)长方体的长、宽、高分别为3厘米、2厘米和1 3=3(厘米)。表面积为(3 2 3 3 2 3 ) 2=42 (cm2)。
这个问题有三种答案。绘画在检查和理解问题的意义方面起着作用。
03
分析图
一些应用题,为了能正确审题和分析题目中的数量关系,可以把题目中的条件、问题的相互关系用分析图表示出来。例1 新华中学买来 8张桌子和几把椅子,共花了 817.6元。每张桌子价 78.5元,比每把椅子贵 62.7元,买来椅子多少把?
分析图:
(l)买椅子共花多少钱?817.6-78.5×8=189.6元)
(2)每把椅子多少钱?78.5-62.7=15.8(元)
(3)买来椅子多少把?189.6÷15.8=12(把)
综合算式为:(817.6-78.5×8)÷(78.5-62.7)
=189.6÷15.8
=12(把)
答:买来椅子12把。
04
线段图
一些题目条件多,条件之间关系复杂,一时难以解答。可画线段图表示,寻求解题的突破口。
例1 光明小学六年级毕业生比全校总人数的
还多30人。新学期一年级新生入数360人,这样现在比原全校总人数增加了
。求原来全校学生有多少人?
从图中可以清楚看出,(360-30)人与全校人数的(
)相对应,求全校人数用除法计算。列式为:
(360-30)÷(
)=330÷=900(人)。
例2 甲乙两人同时从相距88千米的两地相向而行,8小时后在距中点4千米处相遇。甲比乙速度快,甲、乙每小时各行多少千米?
按照题意画线段图:
从图中可以清楚看出,甲、乙8小时各行的距离,甲行全程的一半又多出 4千米,乙行全程的一半少 4千米,这样就可以求出甲、乙的速度了。
甲速:(88÷2+4)÷8=6(千米)
乙速:(88÷2-4)÷8=5(千米)
05
表格图
有些问题,通过列表不仅能分清题目的条件和问题,而且便于区分比较,起到良好的审题作用。
例1 小明3次搬运15块砖,照这样计算,小明又搬了4次,共搬多少块砖?
根据条件、问题,列出易懂的表格,能清楚看出已知条件和所求问题。
3次
15块
又搬4次
共搬?块
从表中不难看出,又搬4次和共搬多少块,这两个数量不相对应,要先求一共搬多少次,才能求出共搬多少块,列式为:
15÷3×(3+4)=35(块)
另一种思路为,先求又搬4次搬的块数,再加上原有的块数,就是共搬的块数。列式为:
15÷3×4+15=35(块)
06
思路图
有些问题因为分析的角度不同,因此解题的思路也不同。通过画图能清楚看出解题思路,便于分析比较。
例1 有一个伍分币、4个贰分币、8个壹分币,要拿出8分钱,一共有多少种拿法?
这道题从表面港一点也不难,但是要不重复。不遗漏地把全部拿法一一说出来也不容易,可以用枚举法把各种情况一一列举出来,把思路写出来。
从图表中可以清楚着出不同的拿法。此题一共有不重复的7种拿法。
从以上各例题中可看出:解题时通过画图来帮助理解题意,起到了化繁为简、化难为易的作用。我们不妨在解题中广泛使用。