统计学:中方差和偏离基准的定义
方差是什么? 电子表格的大小显示了一列。
每个数据和标准偏差是什么?平均值之间的距离是与标准的偏差。
在机器学习方差中,我们可以确定单个列的记录是否分散,或者换句话说,是否远离数据集的意义。
方差计算公式
标准偏差计算公式
在希腊被称为Sigma。
通过示例计算方差和与标准偏差
我们用一个例子来看一下。
在这个例子中,引入了几只狗,它们想利用差异来测量狗的状况。
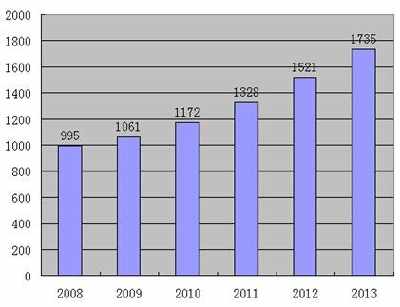
每只狗离肩(胫骨)的高度分别为600毫米、470毫米、170毫米、430毫米和300毫米。我们的任务是获取方差、标准差和平均值。
平均值=(600 470 170 430 300)/5=
平均值=1970/5=
平均值= 395
因此,上图中的平均值如下:
平均视图(绿线表示平均)
现在用平均值计算每只狗的身高差,如下:
每只狗的身高和平均值的差值
现在我们必须计算它们之间的差异:
方差计算方法
现在,如果我们取方差的根,我们把标准差:
/pgc-image/0f5ab822f3af4e6db6485af482b47000" />计算标准偏差
现在我们可以更新我们的形状:
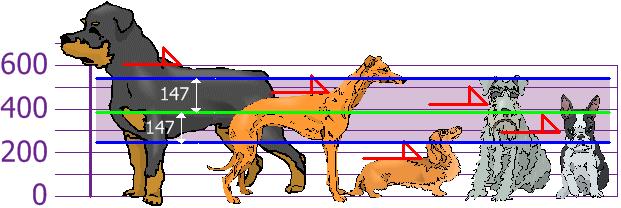
计算狗之间的标准差
现在我们可以轻松确定哪种标准适合我们。左边的狗不是我们的标准,它们已经高于标准,中间的犬是最矮的狗,也不在我们这个数据集的标准中。
注意:关键是当方差很小并且接近于零时,这意味着列的记录非常接近平均值并且彼此非常接近。高方差告诉我们,有多少记录是平均值的支柱,彼此之间相差甚远。
学习机器的方差概念:
这是方差和标准偏差的最简单定义。但这种外观只是一种统计外观,而不是数据科学家。作为数据科学家,您需要了解方差对机器学习的影响。
所以我们有两个概念:
低差异:告诉您数据集中的最小变化会导致结果在目标函数中发生变化。
高差异:告诉您必须发生重大变化,以使目标函数在其估计值中发生变化。
机器学习中的低方差的示例包括线性回归,线性分析,线性逻辑回归和逻辑回归。
机器学习中的高方差的示例包括决策树,K邻近邻居(K-Nearby Neighbor)和支持向量机。
最后,在计算方差和标准偏差时,可能会遇到样本和总体两个概念:
在谈论我们的样本和总体时,我们实际上想在我最初为您提供的公式中讨论N. 让我们看一下与一组狗相同的例子。如果我们的整个数据集具有相同数量的狗,我们将方差除以该集合的列中的记录总数,其中五个(总共五只狗)。如果这个狗的数量是一个更大的数据集的一个例子,我们应该在公式中加入N-1,而不是n.所以:
什么是总体?我们计算总体数据集列的总记录。
什么是样本?要从示例数据集计算列的多个记录。
样本中的是不需要统计数据的,需要的是计算整个数据集。模式的唯一索引为我们提供了最多的信息。但是也要考虑使用样本会失去在数据集中的准确度,但是却减少了很多时间。
最后,这里有;两种偏离公式的算法:

两种显示偏离公式的方法