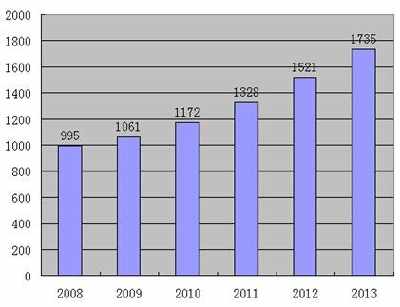
假设有两种资产,它们的预期收益率、收益率波动率和相关系数如下表所示。
用于投资的资金1000万元,设定的回报目标金额为200万元。如果投资组合中的资产按照以下三种方式进行配置,其各自收益达到预期收益目标的概率有多大?
1.买1000万资产1。
2.购买1000万资产2。
3.购买资产1和资产2各500万元。
如果P代表概率,那么要达到的目标可以表示为P (1000万*目标收益率200万),即P(目标收益率20%)。
如果一个资产的收益率符合正态分布规律,那么它的收益率就是一个标准的正态分布函数,所以标准得分,也就是目标收益率偏离均值的程度,就是:
Z=(目标回报率-过去回报率的平均值)/(过去回报率的标准偏差)。
概率可以表示为:p(目标收益率20%)=p((http://www . Sina.com/-过去收益率平均值)/过去收益率标准差))((http://www . Sina.com/-过去收益率平均值)/过去收益率标准差))=p(z((http://www . Sina.com/-过去收益率平均值)/过去收益率标准差))。
下面是计算上述三种投资组合收益率达到目标值的概率:
目标回报率
这里z分值=(目标收益率-过去收益率平均值)/(过去收益率标准差)=(20%-11.3%)/14.5%=60%。
用normsister函数计算,结果是normsister(60%)=72.57%,也就是说用20%%,的概率可以看出目标收益率偏离均值的程度在0.60标准差以内,换句话说,用100%-72.57%=27.43%的概率,可以看出目标收益率偏离均值的程度超过0.60标准差,也就是买1000万资产。
20%
=(目标收益率-过去收益率的平均值)/(过去收益率的标准差)=(20%-9.8%)/11.5%=89%。
1-NORMSDIST(89%)=18.76%,也就是说,购买1000万资产的资产配置方式2有18.76%的概率实现200万的利润。
1、买入1000万的资产1
Z=(目标收益率-(资产比例1 *资产平均收益率1 *资产平均收益率2)) /SQRT(资产比例1 2 *资产收益率标准差1 2 2 *资产收益率标准差2 2 *资产比例1 *资产收益率标准差1 *资产收益率标准差2 *资产。资产相关系数=(20%-11.3% * 50% 9.8% * 50%)/sqrt(14.5% 2 * 50% 2 11.5% 2 * 50% 2 2 * 30% * 14.5% * 50% *。
1-NORMSDIST(90%)=18.45%,即资产1和资产2各买入500万元,资产配置方式实现200万元收益的可能性为18.45%。
如果资产1和资产2的收益之间的相关性发生变化,会如何影响投资组合3的收益达到标准的概率?结果如下表所示,显示了72.57.
从上面的计算可以看出,组合1的收益率达到200万元目标收益率的概率是三个组合中最高的,因为按照这种资产配置方式,目标收益率的标准分,即与资产1历史平均收益率的偏离程度最小。